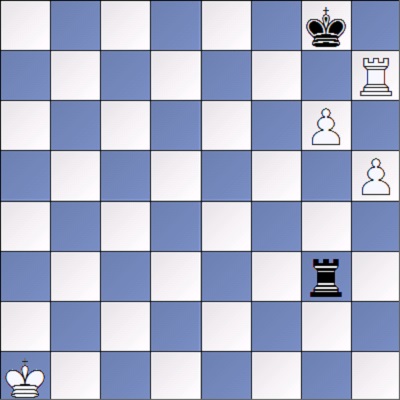
Kasparian es el autor del estudio que vamos a ver a continuación, veamos como podemos formular reglas para ese final. El blanco para progresar necesita defender su peón desde la quinta fila. Para evitar esto la torre negra está sujeta a las columnas g y h moviendo alternativamente entre g3 y h3. Si inicialmente la torre mueve a Tb7 se responde Tg5. El blanco para intentar sacar la torre de las dos columnas, deberá pedir ayuda al rey, pero con cuidado de echar a la torre sin entrar en la columna g. Veamos la posición final a la que hay que llegar para conseguir extraer la torre.
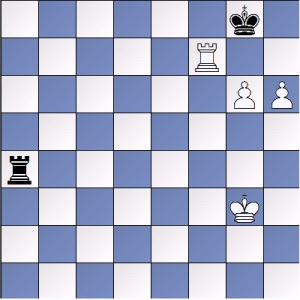
Esta es posición de zugzwang mutuo, en caso de mover las blancas hacen tablas, en caso de mover las negras, ganan las blancas
Si ahora le toca mover a las negras, veamos que el rey negro no se puede mover con 1…Rf8 2.Rg2.Th4 3.Rg3,Ta4 5.Tf7+ Rg8 6.h6.
Si la torre negra se mueve por su fila, la torre blanca aprovechara para ir a defender en dos jugadas a la fila 5; si la ocupa la torre negra, simplemente h6 amenaza mate y la partida se pierde. Si la torre negra se mueve por h, el rey blanco juega Rg3 camino de defender sus peones o refugiarse en h6, de cualquier forma gana.
Si ahora le toca mover a las blancas, 1.Rf2, Ta6 2.Tb7, Ta5
3.h6,Tg5+= o bien tiene que retroceder la torre blanca a 3.Th7,Ta6=
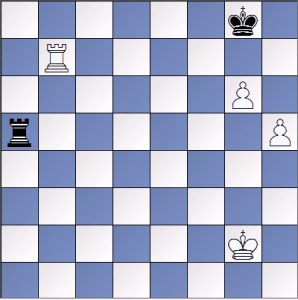
Volvamos a la posición inicial
Como hemos dicho en el inicio, la torre está obligada a moverse entre g3 (casilla negra) y h3 (casilla blanca), en la posición final el rey está en casilla negra y la torre en casilla blanca (distinto color). Si el rey blanco en la primera jugada va a casilla blanca (de color contrario), esta regla de colores contrarios, se cumplirá hasta el final. Es por esto que las blancas ganan en la posición inicial con Ra7 y hacen tablas con Rb7. En estos tres artículos hemos visto casos en los que el rey, los peones, el caballo o la torre, están obligados a ir casilla blanca-negra-blanca alternando el color. Que complicado seria el ajedrez si existiesen ademas casillas grises.
