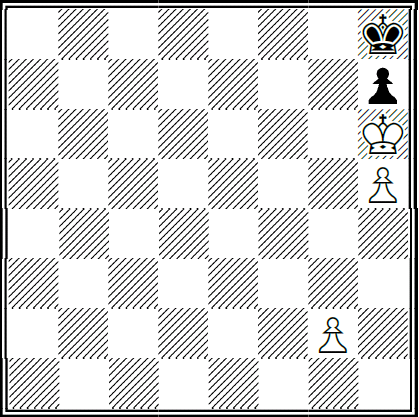
El caballo es la única pieza que cada vez que mueve obligatoriamente pasa a una casilla de distinto color. Si está en casilla blanca salta a negra y por lo tanto ataca a una casilla blanca y viceversa. En este estudio el rey blanco para empatar debe de ir a una de las dos casillas (c1 y c2, negra y blanca) que obstruyen la salida al rey negro y ademas no permitir que el caballo se lo impida.
Para que esto ocurra, el rey debe dejar que cuando el negro mueva el caballo este le de jaque, de esta forma puede ir a la otra de las dos casillas, ¿como se logra sin demasiados cálculos? . Antes hemos dicho que el caballo va a ir a casillas que van cambiando de color, y esto ocurrirá igual con el rey blanco siempre que quiera el blanco. En este caso si el blanco quiere que le den jaque deberá ir primero a c1 de color negro igual que la casilla del caballo. Moviéndose después entre c1 y c2, el rey estará siempre en una casilla del mismo color que el caballo y el caballo al mover le podrá dar jaque, pero no podrá atacar la otra casilla y obligar al rey a salir de esas dos casillas críticas.
Seguramente muchos ajedrecistas saben de esta posición y que puede proceder de una de alfil contra caballo y peón de torre. Vamos a ver como el negro puede hacer que el blanco llegue a un zugzwang y ganar. Para ello nos fijamos en la posición final de zugzwang, como se hizo en al artículo anterior «Zugzwang, abstracciones y reglas» .
Si en esta posición le toca jugar a las blancas, deberán jugar 1.Rc3 (casilla mas próxima a c1 y c2) y después de 1…Rxa1 el rey no puede ir a c1 única casilla que le libraría de perder tendría que jugar 2.Rc2, Cd3 y las blancas están perdidas.
A la posición final de zugzwang se puede llegar después de la siguiente:
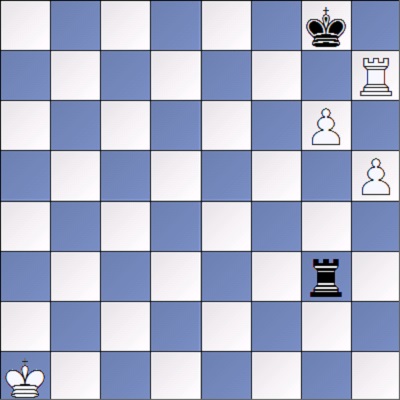
Da igual si el rey blanco este en e1,e2 o e3. Si hemos entendido bien y hacemos una abstracción de la idea anterior podemos solucionar esta situación, en este caso los reyes se encuentran dos columnas movidos a la derecha. La idea del blanco es la misma, ir pegado al negro para bloquear. Cuando el rey negro vaya a b1 el rey blanco deberá ir a d2 (casilla negra igual que el caballo) para que el caballo negro no pueda sacarlo de las casillas d1 y d2 atacando la casilla d1. Para desgracia del blanco existe un doble en b3 que arruinaría el plan. Esta claro que el rey blanco debe de ir a d1. A cualquier retirada del alfil seguiría Ca4 amenazando bloquear con Cb2 , pues si el alfil retrocede con Aa1 el rey negro se lo comería con placer, ya que el rey blanco no llega a tiempo. El rey negro ha roto la regla de ir a una casilla del mismo color del caballo y esto lo pagará caro. Despues de 1…Rb1 2.Rd1,Cd3
Ahora el rey blanco tiene que ir a d2 (casilla negra) si no quiere alejarse y no puede ir a casilla blanca (del mismo color que la del caballo) entonces el caballo con Cb2 ataca a la casilla d1 y obliga al rey blanco a salir fuera de las casillas d1 y d2.
3.Rd2,Cb2
El rey blanco no puede ir a d1. Después de 4.Rc3, Rxb1 el rey blanco tiene que ir a casilla blanca 5.Rc2, Cd3
El rey blanco no puede ocupar c1, todo está perdido después de obligar a salir al rey blanco de c1 y c2. Como final del artículo solamente añadir que las ideas surgen y hay que profundizar en ellas para hacer abstracciones y aprovecharlas, es una lastima que se juegue con reloj.