La posición de Zugzwang es conocida por la mayoría de los ajedrecistas. En dicha posición, al que le toca mover le gustaría pasar, porque si juega pierde. Se produce con mucha frecuencia en los finales. En esta fase del juego es más fácil llegar a ella, ya que los recursos de los jugadores se han reducido mucho y el juego se ha focalizado en un punto. Los temas en los que se produce pueden ser: el paso de un rey, una ruptura, una pieza sobrecargada que ha de mover, restricciones de banda, etc.
En los finales como en cualquier tipo de problemas, sean o no de ajedrez, hay que empezar a resolverlos por el final. Hay que ver qué posición nos lleva a la victoria y tratar de llegar a ella. Cuando se sabe donde llegar, se traza el plan o la estrategia.
A veces cuando los movimientos posibles son reducidos se pueden generar reglas que simplifiquen el cálculo, como la regla del cuadrado para el rey contra peón pasado. A continuación vamos a exponer algunos ejemplos de lo dicho.
Regla de Bird

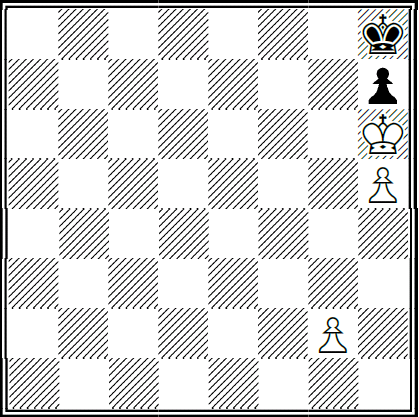
La siguiente posición es de Zugzwang mutuo, si mueve el negro pierde y si le toca al blanco hace tablas. Conociendo el resultado de esta posición final, vamos a ver la siguiente posición, en la que juega el blanco.
El peón blanco tiene la solución al poder mover una o dos casillas. El procedimiento normal sería el cálculo de las jugadas. Sin embargo, podemos aplicar una regla que se cumple en todo el proceso después de la jugada inicial. El peón blanco va de una casilla blanca a una negra y el rey exactamente lo mismo. Si queremos llegar g6 (casilla blanca) con el rey negro en h8 (casilla negra) , la primera jugada a de ser g4 (casilla blanca).
Si el rey estuviera en g8 (casilla blanca) el peón blanco debería ir g3 (casilla negra) para ganar.
Ya tenemos la regla, el peón blanco a de ir a la casilla del color contrario, pues esto se mantiene hasta la posición de zugzwang. Hemos hecho una abstracción que nos vale para las dos posiciones del rey (g8 y h8).
Sigamos avanzando en el estudio con la siguiente posición.
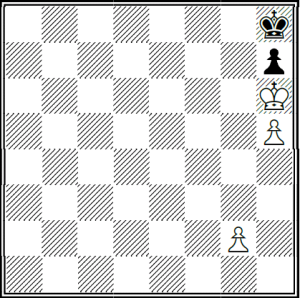
Si el peón de g estuviera en g5 y tocase jugar a las blancas, ganarían por lo visto anteriormente. Hagamos el mismo razonamiento de antes. Si el peón de h fuera de uno en uno, a peón en negro le corresponde rey en negro y viceversa. Esto no interesa pues a peón en h5 corresponde rey en g8 y lo necesitamos en h8. Es por eso que el peón de h hay que moverlo dos casillas, así el peón y el rey quedarían en colores distintos después de mover el negro, que es lo que nos interesa.
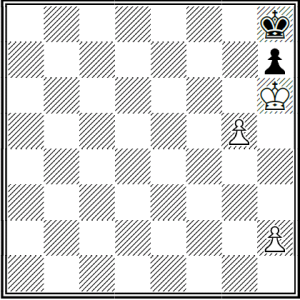
Hemos visto que en la posición siguiente se gana si juegan negras.
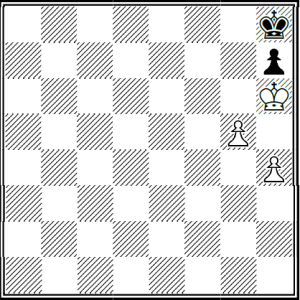
Aquí podemos ver la idea de Bird, los reyes en cada jugada alternaran y pasaran de estar en casillas de igual color a casillas de distinto color. A los peones blancos les ocurre lo mismo entre ellos. Luego si los reyes están en casillas del mismo color al mover un peón las blancas, los peones deben de quedar en casillas de igual color y así la victoria está asegurada pues la regla se cumple hasta el final.

En la anterior posición se gana simplemente haciendo h3, los peones quedan en colores distintos como lo están los reyes. El rey negro pasa a continuación a estar en el mismo color que el rey blanco pero al mover uno de los peones estos quedan en al mismo color. Si nos fijamos en la posición final ganadora esta cumple la regla.
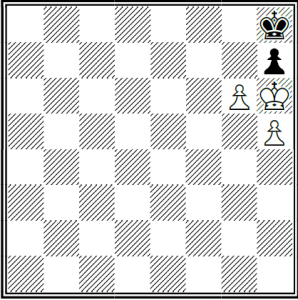
Hay que estudiar la posición final y comprobar si hay alguna regla que se cumple a lo largo de las jugadas, esto nos ayudara a no tener que calcular largas variantes.